Linear buckling analysis of a plate#
Here wee see the first 4 buckling modes of a simply supported plate, generated
using refinement=3 in the script.
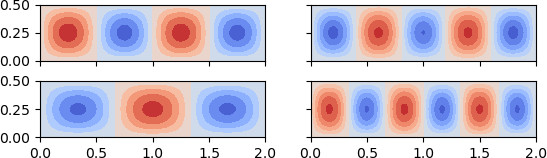
The linear buckling eigenvalue analysis is performed from the fundamental state
calculated after a static analysis. The code used to generate this figure is
extracted from one of pyfe3d unit tests:
import sys
sys.path.append('..')
import numpy as np
from numpy import isclose
from scipy.sparse.linalg import eigsh, spsolve, cg
from scipy.sparse import coo_matrix
from pyfe3d.shellprop_utils import isotropic_plate
from pyfe3d import Quad4R, Quad4RData, Quad4RProbe, INT, DOUBLE, DOF
def test_linear_buckling_plate(plot=False, mode=0, refinement=1):
data = Quad4RData()
probe = Quad4RProbe()
nx = refinement*31
ny = refinement*15
if (nx % 2) == 0:
nx += 1
if (ny % 2) == 0:
ny += 1
a = 2.0
b = 0.5
E = 203.e9 # Pa
nu = 0.33
rho = 7.83e3 # kg/m3
h = 0.003 # m
xtmp = np.linspace(0, a, nx)
ytmp = np.linspace(0, b, ny)
xmesh, ymesh = np.meshgrid(xtmp, ytmp)
ncoords = np.vstack((xmesh.T.flatten(), ymesh.T.flatten(), np.zeros_like(ymesh.T.flatten()))).T
x = ncoords[:, 0]
y = ncoords[:, 1]
z = ncoords[:, 2]
ncoords_flatten = ncoords.flatten()
nids = 1 + np.arange(ncoords.shape[0])
nid_pos = dict(zip(nids, np.arange(len(nids))))
nids_mesh = nids.reshape(nx, ny)
n1s = nids_mesh[:-1, :-1].flatten()
n2s = nids_mesh[1:, :-1].flatten()
n3s = nids_mesh[1:, 1:].flatten()
n4s = nids_mesh[:-1, 1:].flatten()
num_elements = len(n1s)
print('num_elements', num_elements)
KC0r = np.zeros(data.KC0_SPARSE_SIZE*num_elements, dtype=INT)
KC0c = np.zeros(data.KC0_SPARSE_SIZE*num_elements, dtype=INT)
KC0v = np.zeros(data.KC0_SPARSE_SIZE*num_elements, dtype=DOUBLE)
KGr = np.zeros(data.KG_SPARSE_SIZE*num_elements, dtype=INT)
KGc = np.zeros(data.KG_SPARSE_SIZE*num_elements, dtype=INT)
KGv = np.zeros(data.KG_SPARSE_SIZE*num_elements, dtype=DOUBLE)
N = DOF*nx*ny
prop = isotropic_plate(thickness=h, E=E, nu=nu, calc_scf=True, rho=rho)
quads = []
init_k_KC0 = 0
init_k_KG = 0
for n1, n2, n3, n4 in zip(n1s, n2s, n3s, n4s):
pos1 = nid_pos[n1]
pos2 = nid_pos[n2]
pos3 = nid_pos[n3]
pos4 = nid_pos[n4]
r1 = ncoords[pos1]
r2 = ncoords[pos2]
r3 = ncoords[pos3]
normal = np.cross(r2 - r1, r3 - r2)[2]
assert normal > 0
quad = Quad4R(probe)
quad.n1 = n1
quad.n2 = n2
quad.n3 = n3
quad.n4 = n4
quad.c1 = DOF*nid_pos[n1]
quad.c2 = DOF*nid_pos[n2]
quad.c3 = DOF*nid_pos[n3]
quad.c4 = DOF*nid_pos[n4]
quad.init_k_KC0 = init_k_KC0
quad.init_k_KG = init_k_KG
quad.update_rotation_matrix(ncoords_flatten)
quad.update_probe_xe(ncoords_flatten)
quad.update_KC0(KC0r, KC0c, KC0v, prop)
quads.append(quad)
init_k_KC0 += data.KC0_SPARSE_SIZE
init_k_KG += data.KG_SPARSE_SIZE
print('elements created')
KC0 = coo_matrix((KC0v, (KC0r, KC0c)), shape=(N, N)).tocsc()
print('sparse KC0 and M created')
bk = np.zeros(N, dtype=bool)
check = isclose(x, 0.) | isclose(x, a) | isclose(y, 0) | isclose(y, b)
bk[2::DOF] = check
# constraining u at x = a/2, y = 0,b
check = isclose(x, a/2.) & (isclose(y, 0.) | isclose(y, b))
bk[0::DOF] = check
# constraining v at x = 0,a y = b/2
check = isclose(y, b/2.) & (isclose(x, 0.) | isclose(x, a))
bk[1::DOF] = check
# removing drilling
bk[5::DOF] = True
bu = ~bk
# applying load along u at x=a
# nodes at vertices get 1/2 of the force distribution
fext = np.zeros(N)
ftotal = -1000.
print('ftotal', ftotal)
# at x=0
check = (isclose(x, 0) & ~isclose(y, 0) & ~isclose(y, b))
fext[0::DOF][check] = -ftotal/(ny - 1)
check = ((isclose(x, 0) & isclose(y, 0))
|(isclose(x, 0) & isclose(y, b)))
fext[0::DOF][check] = -ftotal/(ny - 1)/2
assert np.isclose(fext.sum(), -ftotal)
# at x=a
check = (isclose(x, a) & ~isclose(y, 0) & ~isclose(y, b))
fext[0::DOF][check] = ftotal/(ny - 1)
check = ((isclose(x, a) & isclose(y, 0))
|(isclose(x, a) & isclose(y, b)))
fext[0::DOF][check] = ftotal/(ny - 1)/2
assert np.isclose(fext.sum(), 0)
Kuu = KC0[bu, :][:, bu]
fextu = fext[bu]
PREC = np.max(1/Kuu.diagonal())
uu, out = cg(PREC*Kuu, PREC*fextu, atol=1e-8)
assert out == 0, 'cg failed'
u = np.zeros(N)
u[bu] = uu
print('u extremes', u[0::DOF].min(), u[0::DOF].max())
print('v extremes', u[1::DOF].min(), u[1::DOF].max())
print('w extremes', u[2::DOF].min(), u[2::DOF].max())
if False:
import matplotlib.pyplot as plt
plt.gca().set_aspect('equal')
uplot = u[0::DOF].reshape(nx, ny).T
levels = np.linspace(uplot.min(), uplot.max(), 300)
plt.contourf(xmesh, ymesh, uplot, levels=levels)
plt.colorbar()
plt.show()
raise
for quad in quads:
quad.update_probe_ue(u) # NOTE update affects the Quad4RProbe class attribute ue
quad.update_probe_xe(ncoords_flatten)
quad.update_KG(KGr, KGc, KGv, prop)
KG = coo_matrix((KGv, (KGr, KGc)), shape=(N, N)).tocsc()
KGuu = KG[bu, :][:, bu]
print('sparse KG created')
num_eig_lb = max(mode+1, 4)
eigvecs = np.zeros((N, num_eig_lb))
eigvals, eigvecsu = eigsh(A=PREC*KGuu, k=num_eig_lb, which='SM',
M=PREC*Kuu, tol=1e-15, sigma=1., mode='cayley')
eigvals = -1./eigvals
eigvecs[bu] = eigvecsu
load_mult = eigvals[0]
P_cr_calc = load_mult*ftotal
print('linear buckling load_mult =', load_mult)
print('linear buckling P_cr_calc =', P_cr_calc)
# theoretical reference
kcmin = 1e6
mmin = 0
for m in range(1, 21):
kc = (m*b/a + a/(m*b))**2
if kc <= kcmin:
kcmin = kc
mmin = m
print('kcmin =', kcmin)
print('m =', mmin)
sigma_cr = -kcmin*np.pi**2*E/(12*(1-nu**2))*h**2/b**2
P_cr_theory = sigma_cr*h*b
print('Theoretical P_cr_theory', P_cr_theory)
print('eigvals', eigvals)
if plot:
import matplotlib.pyplot as plt
fig, axs = plt.subplots(2, 2, sharex=True, sharey=True)
axs[0, 0].set_aspect('equal')
axs[0, 0].contourf(xmesh, ymesh, eigvecs[2::DOF, 0].reshape(nx, ny).T,
levels=10, cmap='coolwarm')
axs[0, 1].set_aspect('equal')
axs[0, 1].set_aspect('equal')
axs[0, 1].contourf(xmesh, ymesh, eigvecs[2::DOF, 1].reshape(nx, ny).T,
levels=10, cmap='coolwarm')
axs[1, 0].set_aspect('equal')
axs[1, 0].contourf(xmesh, ymesh, eigvecs[2::DOF, 2].reshape(nx, ny).T,
levels=10, cmap='coolwarm')
axs[1, 1].set_aspect('equal')
axs[1, 1].contourf(xmesh, ymesh, eigvecs[2::DOF, 3].reshape(nx, ny).T,
levels=10, cmap='coolwarm')
plt.show()
assert isclose(P_cr_theory, P_cr_calc, rtol=0.05)
if __name__ == '__main__':
test_linear_buckling_plate(plot=True, mode=0, refinement=3)