Linear buckling analysis of a cylinder under torsion#
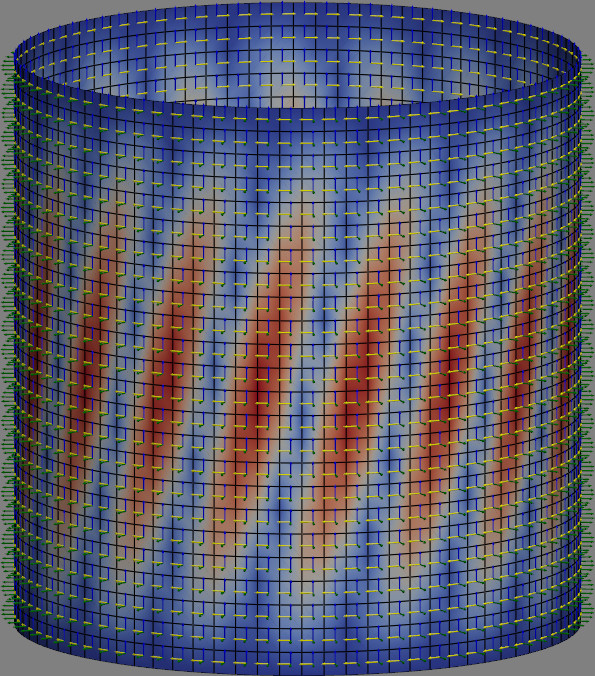
The figure below shows the first linear buckling mode of a cylindrical shell
under torsion. Note that the local coordinates of each element are also
plotted, all using PyVista. The figure was generated using refinement=2 and
running the script directly.
The code used to generate this figure is extracted from one of pyfe3d unit
tests:
import sys
sys.path.append('..')
import time
import numpy as np
from numpy import isclose
from scipy.sparse.linalg import eigsh, spsolve
from scipy.sparse import coo_matrix
from pyfe3d.shellprop_utils import laminated_plate
from pyfe3d import Quad4, Quad4Data, Quad4Probe, INT, DOUBLE, DOF
def test_linear_buckling_cylinder_Nxy(mode=0, plot_pyvista=False, refinement=1):
r"""Test case from reference
Saullo G. P. Castro, Christian Mittelstedt, Francisco A. C. Monteiro, Mariano
A. Arbelo, Gerhard Ziegmann, Richard Degenhardt. "Linear buckling predictions
of unstiffened laminated composite cylinders and cones under various loading
and boundary conditions using semi-analytical models". Composite Structures,
2014. 10.1016/j.compstruct.2014.07.037
Cylinders Z11 and Z33 are used given their distinct torsion buckling
behaviour.
"""
# NOTE in Fig. 1 of Castro's paper that in their coordinate system a
# positive angle should be represented also a positive angle here
# NOTE stacking sequences from Table 4 in Castro et al.
stacks = {
# NOTE actual values from reference can be found here https://github.com/saullocastro/compmech/blob/e7e5342bf212743e70da22c94cc0452911099db3/compmech/conecyl/conecylDB.py#L334
'Z11' : [+60, -60, 0, 0, +68, -68, +52, -52, +37, -37],
# NOTE actual values from reference can be found here https://github.com/saullocastro/compmech/blob/e7e5342bf212743e70da22c94cc0452911099db3/compmech/conecyl/conecylDB.py#L145
'Z33' : [0, 0, 19, -19, 37, -37, 45, -45, 51, -51],
}
# NOTE reference values match with Fig. 13, FSDT CC2, of Castro et al.
reference_Tcr_value_Castro_refinement_8 = {
'Z11' : -19200.8,
'Z33' : -11109.2
}
# NOTE values used for CI tests, values derived after running the tests in
# a local compuer with refinement=8 first and then with refinement=1
reference_Tcr_value_Castro_refinement_1 = {
'Z11' : -32132.3,
'Z33' : -22377.4
}
for cyl in ['Z11', 'Z33']:
stack = stacks[cyl]
ref_Tcr = reference_Tcr_value_Castro_refinement_1[cyl]
data = Quad4Data()
probe = Quad4Probe()
L = 0.510 # m
R = 0.250 # m
b = 2*np.pi*R # m
ntheta = 40*refinement # circumferential
nlength = int(ntheta*L/b)
if nlength % 2 == 0:
nlength += 1
print('ntheta', ntheta)
print('nlength', nlength)
# NOTE material proporties from Table 3 in Castro et al.
# Actual values from reference can be found here https://github.com/saullocastro/compmech/blob/e7e5342bf212743e70da22c94cc0452911099db3/compmech/conecyl/conecylDB.py#L32C34-L32C76
E11 = 123.55e9
E22 = 8.708e9
nu12 = 0.319
G12 = 5.695e9
G13 = 5.695e9
G23 = 3.400e9
plyt = 0.125e-3
laminaprop = (E11, E22, nu12, G12, G13, G23)
prop = laminated_plate(stack=stack, plyt=plyt, laminaprop=laminaprop,
calc_scf=True)
# NOTE forcing 5/6 according to Castro et al., beginning of Section 6
prop.scf_k13 = 5/6
prop.scf_k23 = 5/6
nids = 1 + np.arange(nlength*(ntheta+1))
nids_mesh = nids.reshape(nlength, ntheta+1)
nids_mesh[:, -1] = nids_mesh[:, 0]
nids = np.unique(nids_mesh)
nid_pos = dict(zip(nids, np.arange(len(nids))))
zlin = np.linspace(0, L, nlength)
thetatmp = np.linspace(0, 2*np.pi, ntheta+1)
thetalin = np.linspace(0, 2*np.pi-(thetatmp[-1] - thetatmp[-2]), ntheta)[::-1]
zmesh, thetamesh = np.meshgrid(zlin, thetalin)
zmesh = zmesh.T
thetamesh = thetamesh.T
xmesh = np.cos(thetamesh)*R
ymesh = np.sin(thetamesh)*R
ncoords = np.vstack((xmesh.flatten(), ymesh.flatten(), zmesh.flatten())).T
ncoords_flatten = ncoords.flatten()
x = ncoords[:, 0]
y = ncoords[:, 1]
z = ncoords[:, 2]
n1s = nids_mesh[:-1, :-1].flatten()
n2s = nids_mesh[1:, :-1].flatten()
n3s = nids_mesh[1:, 1:].flatten()
n4s = nids_mesh[:-1, 1:].flatten()
num_elements = len(n1s)
print('num_elements', num_elements)
KC0r = np.zeros(data.KC0_SPARSE_SIZE*num_elements, dtype=INT)
KC0c = np.zeros(data.KC0_SPARSE_SIZE*num_elements, dtype=INT)
KC0v = np.zeros(data.KC0_SPARSE_SIZE*num_elements, dtype=DOUBLE)
KGr = np.zeros(data.KG_SPARSE_SIZE*num_elements, dtype=INT)
KGc = np.zeros(data.KG_SPARSE_SIZE*num_elements, dtype=INT)
KGv = np.zeros(data.KG_SPARSE_SIZE*num_elements, dtype=DOUBLE)
N = DOF*nlength*ntheta
quads = []
init_k_KC0 = 0
init_k_KG = 0
t0 = time.time()
for n1, n2, n3, n4 in zip(n1s, n2s, n3s, n4s):
quad = Quad4(probe)
quad.n1 = n1
quad.n2 = n2
quad.n3 = n3
quad.n4 = n4
quad.c1 = DOF*nid_pos[n1]
quad.c2 = DOF*nid_pos[n2]
quad.c3 = DOF*nid_pos[n3]
quad.c4 = DOF*nid_pos[n4]
quad.init_k_KC0 = init_k_KC0
quad.init_k_KG = init_k_KG
quad.K6ROT = 10.
quad.update_rotation_matrix(ncoords_flatten, 0., 0., 1.)
quad.update_probe_xe(ncoords_flatten)
quad.update_KC0(KC0r, KC0c, KC0v, prop)
quads.append(quad)
init_k_KC0 += data.KC0_SPARSE_SIZE
init_k_KG += data.KG_SPARSE_SIZE
print('elements created', time.time()-t0)
KC0 = coo_matrix((KC0v, (KC0r, KC0c)), shape=(N, N)).tocsc()
print('sparse KC0 created')
bk = np.zeros(N, dtype=bool)
# NOTE cylinders with CC2 boundary condition as decribed in Table 1 of Castro et al.
bottom_edge = isclose(z, 0)
bk[0::DOF][bottom_edge] = True
bk[1::DOF][bottom_edge] = True
bk[3::DOF][bottom_edge] = True
bk[4::DOF][bottom_edge] = True
top_edge = isclose(z, L)
bk[0::DOF][top_edge] = True
bk[1::DOF][top_edge] = True
bk[3::DOF][top_edge] = True
bk[4::DOF][top_edge] = True
middle = isclose(z, L/2)
bk[2::DOF][middle] = True
bu = ~bk
# NOTE in Fig. 1 of Castro et al. that a positive torque (T) represents a
# negative distributed shear force Nxy. This must be consistent with the
# sign of the stacking sequence angles given that it significantly
# influences the results for torsion buckling.
#
Nxy = -1000/b
print('Nxy', Nxy)
for quad in quads:
quad.update_probe_xe(ncoords_flatten) # NOTE update affects the Quad4Probe class attribute xe
quad.update_KG_given_stress(0, 0, Nxy, KGr, KGc, KGv)
KG = coo_matrix((KGv, (KGr, KGc)), shape=(N, N)).tocsc()
KC0uu = KC0[bu, :][:, bu]
KGuu = KG[bu, :][:, bu]
PREC = 1.
print('sparse KG created')
num_eig_lb = max(mode+1, 3)
eigvecs = np.zeros((N, num_eig_lb))
eigvals, eigvecsu = eigsh(A=PREC*KGuu, k=num_eig_lb, which='SM',
M=PREC*KC0uu, tol=1e-6, sigma=1., mode='cayley')
eigvals = -1./eigvals
eigvecs[bu] = eigvecsu
print('eigvals', eigvals)
print('linear buckling analysis OK')
Tcr = eigvals[0]*Nxy*b*R
print('Tcr =', Tcr)
if plot_pyvista:
import pyvista as pv
contour_colorscale = 'coolwarm'
background = 'gray'
vector = eigvecs[:, mode]
contour_label = 'Radial displacement'
contour_vec = np.sqrt(vector[0::DOF]**2 + vector[1::DOF]**2)
displ_vec = np.zeros_like(ncoords)
displ_vec[:, 0] = vector[0::DOF]*10
displ_vec[:, 1] = vector[1::DOF]*10
displ_vec[:, 2] = vector[2::DOF]*10
intensitymode = 'vertex'
plotter = pv.Plotter(off_screen=False)
faces_quad = []
for q in quads:
faces_quad.append([4, nid_pos[q.n1], nid_pos[q.n2], nid_pos[q.n3], nid_pos[q.n4]])
faces_quad = np.array(faces_quad)
quad_plot = pv.PolyData(ncoords, faces_quad)
if contour_vec is not None:
quad_plot[contour_label] = contour_vec
plotter.add_mesh(quad_plot, scalars=contour_label,
cmap=contour_colorscale, edge_color='black', show_edges=True,
line_width=1.)
else:
plotter.add_mesh(quad_plot, edge_color='black', show_edges=True,
line_width=1.)
displ_vec = None
if displ_vec is not None:
quad_plot = pv.PolyData(ncoords + displ_vec, faces_quad)
plotter.add_mesh(quad_plot, edge_color='red', show_edges=True,
line_width=1., opacity=0.5)
#NOTE plotting coordinate system
xaxis = pv.Arrow(start=(0, 0, 0), direction=(1, 0, 0), scale=R/3)
plotter.add_mesh(xaxis, color='blue')
yaxis = pv.Arrow(start=(0, 0, 0), direction=(0, 1, 0), scale=R/3)
plotter.add_mesh(yaxis, color='yellow')
zaxis = pv.Arrow(start=(0, 0, 0), direction=(0, 0, 1), scale=R/3)
plotter.add_mesh(zaxis, color='green')
for q in quads:
pos1 = nid_pos[q.n1]
pos2 = nid_pos[q.n2]
pos3 = nid_pos[q.n3]
pos4 = nid_pos[q.n4]
centroid = (ncoords[pos1] + ncoords[pos2] + ncoords[pos3] + ncoords[pos4])/4
ze = np.array([0., 0., 1.])
zg = np.array([[q.r11, q.r12, q.r13],
[q.r21, q.r22, q.r23],
[q.r31, q.r32, q.r33]]) @ ze
normal = pv.Arrow(start=centroid, direction=zg, scale=R/20)
plotter.add_mesh(normal, color='green')
xe = np.array([1., 0., 0.])
xg = np.array([[q.r11, q.r12, q.r13],
[q.r21, q.r22, q.r23],
[q.r31, q.r32, q.r33]]) @ xe
x_axis = pv.Arrow(start=centroid, direction=xg, scale=R/20)
plotter.add_mesh(x_axis, color='blue')
ye = np.array([0., 1., 0.])
yg = np.array([[q.r11, q.r12, q.r13],
[q.r21, q.r22, q.r23],
[q.r31, q.r32, q.r33]]) @ ye
y_axis = pv.Arrow(start=centroid, direction=yg, scale=R/20)
plotter.add_mesh(y_axis, color='yellow')
plotter.set_background(background)
plotter.parallel_projection = True
plotter.show()
assert np.isclose(Tcr, ref_Tcr, rtol=1e-3)
if __name__ == '__main__':
test_linear_buckling_cylinder_Nxy(mode=0, plot_pyvista=True, refinement=2)